re+RSA
大三上真的忙成狗,感觉比996还累。太久没打CTF了,十分珍惜这次CTF比赛机会(然并卵)。无名也很久没打了,他说他python都有点忘记怎么整了,我笑了笑,去复习gmpy2的用法了,手动微笑。也许是大三上最后一次CTF吧,详细记录一下。赛后RSA问了一下电科的师傅2333,感谢感谢,回答了我的弱智问题。
HideAndSeek
先说结论,老实人做题法肯定遭不住,测信道就完事儿啦
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| import subprocess
import os
import logging
import json
logging.basicConfig(level=logging.INFO)
logger = logging.getLogger(__name__)
class shell(object):
def runCmd(self, cmd):
res = subprocess.Popen(cmd, shell=True, stdin=subprocess.PIPE,
stdout=subprocess.PIPE, stderr=subprocess.STDOUT)
sout, serr = res.communicate()
return res.returncode, sout, serr, res.pid
def initPin(self, cmd):
res = subprocess.Popen(cmd, shell=True, stdin=subprocess.PIPE,
stdout=subprocess.PIPE, stderr=subprocess.STDOUT)
self.res = res
def pinWrite(self, input):
self.res.stdin.write(input)
def pinRun(self):
sout, serr = self.res.communicate()
return sout, serr
filename = "/home/chenyuxin/Desktop/1t"
cmd = "/media/psf/Home/pintool_linux/pin -t " + \
"/media/psf/Home/pintool_linux/source/tools/ManualExamples/obj-intel64/inscount0.so " + " -- " + filename
cout_old = 0
shell = shell()
shell.initPin(cmd)
cout_old=0
flag = 'EIS{you_should_go_for_nascondino_world'
for i in range(256):
for ch in range(128,30,-1):
flag2 = flag + chr(ch)
shell.initPin(cmd)
shell.pinWrite(flag2)
sout,serr = shell.pinRun()
cout = sout.split("Count ")[1]
cout_sub= int(cout) - cout_old
cout_old = int(cout)
print ("current char ", chr(ch),"current count:",cout,"sub_count ",cout_sub)
if ch != 30 and cout_sub > 1000:
flag += chr(ch)
print flag
break
|
老实人们和我一起来看看逻辑吧 : )

首先,是异或解密代码
调试,走进解密代码后,惊喜吗,还是异或解密

憋调了,在输入下内存断点吧,当程序读取输入的时候,肯定是代码解密完了的时候嘻嘻

内存断点安排
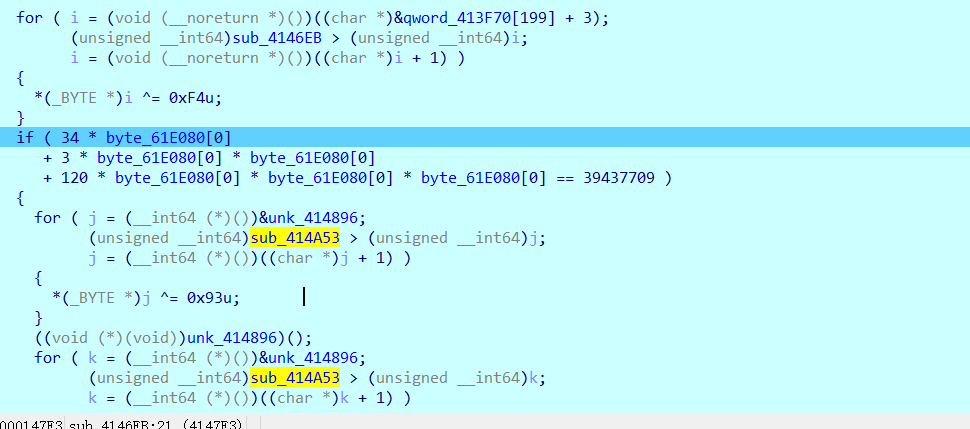
可以看到,走进辽验证函数。给力。
但是继续调试你会发现,不知道套了多少层。。。不知道出题人的源码是咋样的,自动化出题吧2333
。所以到了这一步,可以用z3不断添加限制条件,也可以用pintool来莽。
还有道逆向后面发,_aesenc和_aesdec不配套呵呵 坑死了。
RSA
n1,n2不互素,可以提取p。
但是难点在e,phi不互素。gcd(e,phi)==14。
但是我们可以求d14=gmpy2.invert(e/14,phi)。
这样c1^d1=m^14 mod n1啦。
c2^d2=m^14 mod n2。
给力给力,然后要做滴就是用中国剩余定理。
m^14=c1^d1 mod p
m^14=c1^d1 mod q1
m^14=c2^d2 mod q2 因为n1=p*q1,n2=p*q2
所以可以利用上式求出m^14 mod p*q1*q2。别问原理,再问自杀。
然后求m^14 mod q1*q2,惊喜发现gcd(e,(q1-1)(q2-1))=2。所以同理我们
d2=invert(14/2,(q1-1)(q2-1)) //因为得到m^14求m,所以14视为e
(m^14)^d2=m^2 mod q1*q2
开方得到flag,开心
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| import gmpy2
n1=0xcfc59d54b4b2e9ab1b5d90920ae88f430d39fee60d18dddbc623d15aae645e4e50db1c07a02d472b2eebb075a547618e1154a15b1657fbf66ed7e714d23ac70bdfba4c809bbb1e27687163cb09258a07ab2533568192e29a3b8e31a5de886050b28b3ed58e81952487714dd7ae012708db30eaf007620cdeb34f150836a4b723L
e1=0xfae3aL
c1=0x81523a330fb15125b6184e4461dadac7601340960840c5213b67a788c84aecfcdc3caf0bf3e27e4c95bb3c154db7055376981972b1565c22c100c47f3fa1dd2994e56090067b4e66f1c3905f9f780145cdf8d0fea88a45bae5113da37c8879c9cdb8ee9a55892bac3bae11fbbabcba0626163d0e2e12c04d99f4eeba5071cbeaL
n2=0xd45304b186dc82e40bd387afc831c32a4c7ba514a64ae051b62f483f27951065a6a04a030d285bdc1cb457b24c2f8701f574094d46d8de37b5a6d55356d1d368b89e16fa71b6603bd037c7f329a3096ce903937bb0c4f112a678c88fd5d84016f745b8281aea8fd5bcc28b68c293e4ef4a62a62e478a8b6cd46f3da73fa34c63L
e2=0x1f9eaeL
c2=0x4d7ceaadf5e662ab2e0149a8d18a4777b4cd4a7712ab825cf913206c325e6abb88954ebc37b2bda19aed16c5938ac43f43966e96a86913129e38c853ecd4ebc89e806f823ffb802e3ddef0ac6c5ba078d3983393a91cd7a1b59660d47d2045c03ff529c341f3ed994235a68c57f8195f75d61fc8cac37e936d9a6b75c4bd2347L
p=gmpy2.gcd(n1,n2)
q1=n1/p
q2=n2/p
phi1=(p-1)*(q1-1)
phi2=(p-1)*(q2-1)
d1=gmpy2.invert(e1/14,phi1)
d2=gmpy2.invert(e2/14,phi2)
x1=pow(c1,d1,p)
x2=pow(c1,d1,q1)
x3=pow(c2,d2,q2)
M=p*q1*q2
M1=q1*q2
M2=p*q2
M3=p*q1
t1=gmpy2.invert(M1,p)
t2=gmpy2.invert(M2,q1)
t3=gmpy2.invert(M3,q2)
m14=(x1*M1*t1+x2*M2*t2+x3*M3*t3)%M
print m14
d2=gmpy2.invert(14/2,(q1-1)*(q2-1))
m2=pow(m14,d2,q1*q2)
print gmpy2.iroot(m2,2)
flag_num=gmpy2.iroot(m2,2)[0]
print hex(flag_num)[2:].decode('hex')
|
后记
有得有失,希望大三稳住成绩,后面发一些路由器漏洞,后门啥的,有机会填坑re2~。




