2019-0ctf-elements | Stay foolish,stay hungry!

题目

题目逻辑很简单，就是flag{391bc2164f0a -xxxxxxxxxxxx-xxxxxxxxxxxx}格式，字符限制是0-f。

核心

其实就是两个方程组，未知数两个，按理说可以解开。

当然也可以把它当成一个数学问题，海伦公式。已知外接圆半径，内切圆半径，和一边，求剩余两边。

这里我用Matlab解的，佛了，用z3解不出来，把限制条件原封不动搬到Matlab可以出来。

syms y z
x=vpa(eig(62791383142154.0),24) %提高精度
e1=2*0.25*(4.0 * x * x* y * y-(x * x + y * y - z * z)*(x * x + y * y - z * z))^0.5/(x+y+z)-19400354808065.542969
e2=x*y*z/((4.0 * x * x* y * y-(x * x + y * y - z * z)*(x * x + y * y - z * z))^0.5)-47770539528273.90625
[y0,z0] = solve(e1,e2,y,z)

然后得到结果z0=95523798483318.005946313093592575 ，y0=70802074077032.995367926799067969

PS：19400354808065.542969这里不用IDA反编译的数，用16进制得到精度高一点的可能会好一点。如下：

A=hex2num('C2B1A4FF41C1018B')
vpa(eig(A),24)

反推

那么得到y和z的值了，就只需要从xmm反推回输入。

首先把y和z转换为16进制。y=42d019391e61da40 z=42d5b83784e05d80

然后根据一下反推

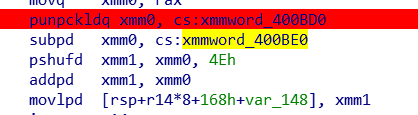
为了方便理解，我们把x的输入的演变记录下来

#0A 4F 16 C2 1B 39 00 00 00 00 00 00 00 00 00 00(state1)->0A 4F 16 C2 00 00 30 43 1B 39 00 00 00 00 30 45 交错排列(state2)->00 00 40 E1 C9 42 E8 41 00 00 00 00 80 8D CC 42相减453000... 433000...(state3)
#->00 00 00 00 80 8D CC 42 00 00 40 E1 C9 42 E8 41交错替换(state4)->00 85 27 0B E1 8D CC 42 00 85 27 0B E1 8D CC 42(state5) state4+state3

16进制的浮点数运算可以参考https://blog.csdn.net/yqj234/article/details/51303712

我们首先可以确定 state5的8D CC 42是state3直接来的，而state3中的00 00 00 00 80 8D CC 42与45300…相加就能直接确定输入的前4位。可以发现42cc8d8000000000作为浮点数与453000…相加的话，80那个位置的影响很小，所以换句话说，我们只用高6位与4530000…相加，得到的结果其实差距不会很大，这里如果用42cc8d00..尝试便知，得到391a。这个方法做下去后两组输入甚至直接能得到正确值。相当于我们能得到state3中的 00 00 00 00 80 8D CC 42，然后用state5减去这个值，就是state3另一部分。最终结果就出来了。

4064e4798769  #56e0de138176

结果