roarctf2019-math
题目介绍
RoarCTF的逆向math是一个几何数学题,看出题人写的出题思路是弦心距极坐标blablabla…
题目:https://github.com/berTrAM888/RoarCTF-Writeup-some-Source-Code/tree/master/Reverse/math
出题人给出的题目设计思路如下:
基于圆的几何问题
所有其他点的坐标都是相对A点的,可以看作坐标系移动了(Ax,Ay)

M,O点坐标已给
输入N点,MN形成弦,计算出弦心距,画一个小圆
然后进入概率check,cnt1和cnt2分别是落在小圆和大圆内的次数
符合概率 反推即 对弦心距的长度有要求
再反推N点相对A点的坐标,N有2解
最后的限制是N在圆上,正好是切点的位置
改:输入的值都进行了极坐标运算,另外添加了ollvm
通过check即给出服务器上的flag
理解几何逻辑后,根据弦心距反推N点即可
1.41421356 5.2057298 0.67083
输入上面这一串以后很大概率成功
最简单的输入A点(1,1)
于是N点坐标即为
//std::cin >> N.x; //N.x = A.x(1) + sqrt(5 + 2 * sqrt(5)); x == 4.07768 //std::cin >> N.y; //N.y = A.y(1) + sqrt(5); y == 3.23607 //转换为极坐标 tan == y/x == 3.23607 / 4.07768 == 0.793606 弧度==0.67083 // ρ == sqrt(27.0996232273) == 5.2057298 长度==5.2057298
//4.07768 3.23607 转换为极坐标后输入有较大可能性通过概率检测
但是其实说到底也就是两个方程,所以可以用matlab这种神器直接解方程,不用去做几何数学(就我的使用体验,对于浮点数的方程来说,matlab的效果比z3好太多了)。
题目逻辑
第一个输入是根号2不多说了,伪代码都可以看得很清楚
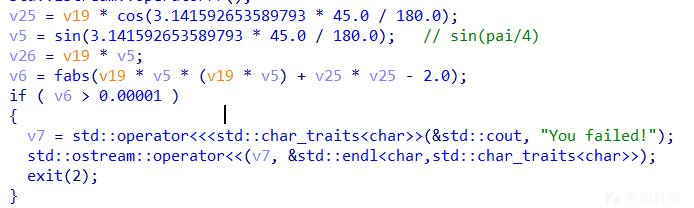
我们设第二个输入是a,第三个输入是b
根据程序后面所使用的,我们令
y=a×cos(b)
z=a×sin(b)
v8=sqrt(10+2×sqrt(5))+sqrt(2)×cos(pi/4)
比较重要的函数是下面这个401049函数。两个不等式都围绕他来展开。
(下图中v29就是y,v30就是z,v27=v28=v8,v26=sqrt(2)*sin(pi/4)=1)

该函数的第一个子函数最好跟汇编,该函数的第一个子函数的返回结果是两个乘积相减

第二个子函数伪代码没什么问题

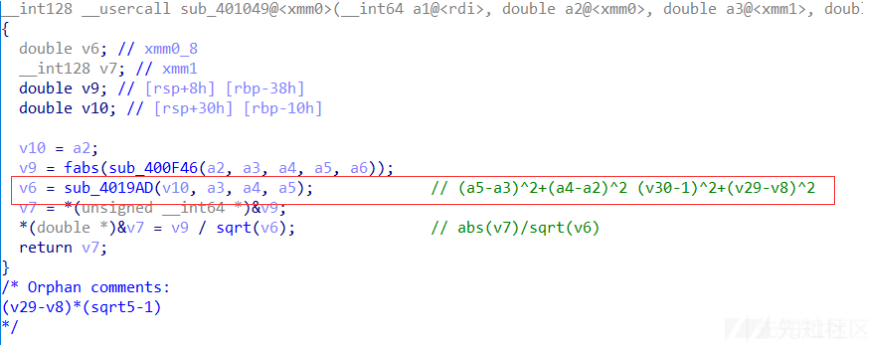
耐心跟一下可以得到第一次调用401049函数的返回值为:
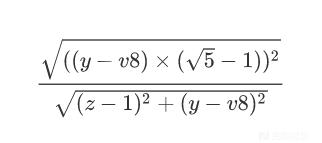
然后该返回值会进入与随机数的比较循环。

这里可以看成是用随机数落在两个圆里的概率比来代表两个圆的面积比。所以可以通过概率比来确定返回值的大小。也就是
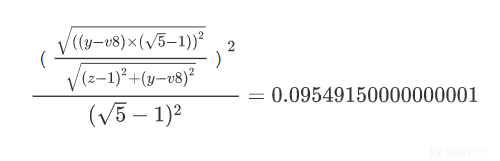
该等式就是我们能获得的第一个等式。
第二个等式也和401049函数有关,v22已知,为sqrt(5)-1

第二次的返回值是
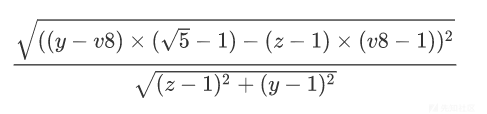
所以应该满足的公式为
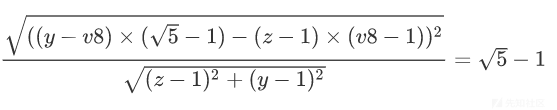
解方程
//matlab
syms y z
v28=vpa(sqrt(10+2 * sqrt(5))+1,24)
e1=(y-v28)^2-0.0954915* ((z-1)^2+(y-v28)^2)
e2=((y-1)* (sqrt(5)-1)-((z-1) * (v28-1)))^2-(sqrt(5)-1)^2 * ((z-1)^2+(y-1)^2)
[y0,z0]=solve(e1,e2,y,z)
得到结果如下
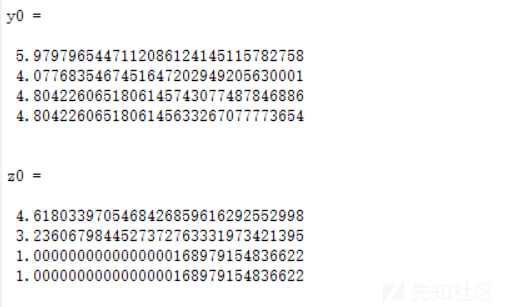
四组可以都试试,最后发现第二组是正确答案(当然带进去稍微跟一下也能确定第二组是正确答案)。
因为y0^2+z0^2可以得到第一个输入的平方:a^2,而z0/y0可以得到第二个输入b的tan值tan(b)。
所以正确输入如下
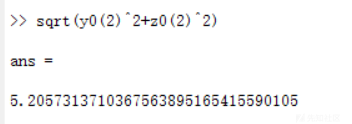
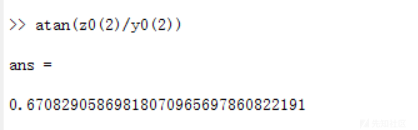
因为满足方程后会执行cat flag,所以在本地我们事先写一个flag文件内容为aaaaaa来进行测试。
注意一下精度的调整便能成功